New Statistical Procedures for Supervised Dimension Reduction
J. Virta, K. Nordhausen, H. Oja
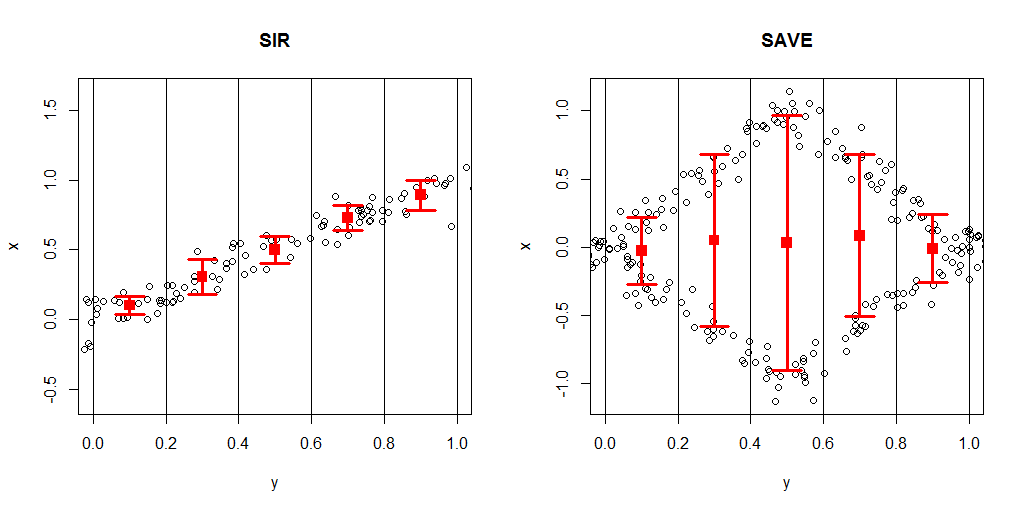
Dimension reduction techniques are frequently utilized when dealing with high dimensional data. The objective of linear dimension reduction is to replace the original variables with a smaller set of linear combinations of them while losing only a minimal amount of information. This is done with a projection matrix P that projects the p-dimensional observations x into a k-dimensional linear subspace determined by P. Additionally, dimension reduction may be unsupervised or supervised. In the latter P is selected so that, given Px, x and some response y are independent, that is, Px carries all the information about the dependence between x and y.
In the thesis work the aim is to consider supervised linear dimension reduction based on the simultaneous diagonalization of two scatter matrices. Often one of the scatter matrices is the regular covariance matrix and the second one carries information about the dependence between x and y. The first objective is to consider the statistical properties (consistency, limiting distribution, robustness, etc.) of the estimates of P under different model assumptions and for different choices of scatter matrices. As a second objective, estimates based on more than two scatter matrices are considered. Finally, tests and estimates for the unknown k will be developed.